PyTorch notes

入门任务：用PyTorch实现MNIST手写数字识别

PyTorch is an optimized tensor library for deep learning using GPUs and CPUs.

导入模块

# 导入PyTorch库
import torch
# torchvision是PyTorch的一个子模块，提供了一些常用的数据集、模型架构和图像转换工具
import torchvision
# 导入DataLoader类，用于加载数据集并生成批次数据
from torch.utils.data import DataLoader
# 导入PyTorch的神经网络模块(neural network)，其中包含了构建神经网络所需的各种层和功能
import torch.nn as nn
# 导入PyTorch的函数模块，其中包含了一些常用的神经网络操作函数，如激活函数、损失函数等
import torch.nn.functional as F
# 导入PyTorch的优化器模块，用于配置和执行优化算法来更新神经网络的参数
import torch.optim as optim
# 导入matplotlib库的pyplot模块，用于绘制图表
import matplotlib.pyplot as plt

参数设置

# 遍历整个训练数据集的次数
n_epochs = 3
# 训练时每个批次的样本数
batch_size_train = 64
# 测试时每个批次的样本数
batch_size_test = 1000
# 学习率，是优化器在更新参数时使用的步长
learning_rate = 0.01
# 动量参数，用于优化器的动量更新
momentum = 0.5
# 每隔多少个批次打印一次训练日志
log_interval = 10
# 定义和设置随机种子
random_seed = 1
torch.manual_seed(random_seed)

learning_rate：学习率，是优化算法中的一个关键超参数，它决定了模型参数在每次迭代中更新的幅度大小。学习率越大，参数更新的步长就越大，模型可能更快地收敛到局部最优解，但也可能导致不稳定性或者错过全局最优解；学习率越小，参数更新的步长就越小，模型收敛速度可能较慢，但可能更容易得到更精确的结果
momentum：在优化算法中，动量参数指定了每次参数更新时，上一步更新的动量对当前更新的影响程度。0.5意思是在每次参数更新时，当前梯度的贡献占50%，而上一步更新的动量占50%
torch.manual_seed(random_seed)设置随机种子，可以使得每次程序运行时生成的随机数序列是一致的，从而使得程序的运行结果可复现。每次运行时都会得到相同的结果，而不会受到随机性的影响，这对于调试和结果验证非常有用

数据集

train_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('./data/', train=True, download=True,
                               transform=torchvision.transforms.Compose([
                                   torchvision.transforms.ToTensor(),
                                   torchvision.transforms.Normalize(
                                       (0.1307,), (0.3081,))
                               ])),
    batch_size=batch_size_train, shuffle=True)

test_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('./data/', train=False, download=True,
                               transform=torchvision.transforms.Compose([
                                   torchvision.transforms.ToTensor(),
                                   torchvision.transforms.Normalize(
                                       (0.1307,), (0.3081,))
                               ])),
    batch_size=batch_size_test, shuffle=True)

download：为True表示如果数据集不存在，则从网络下载
transform=...定义了一系列的数据转换操作，并将它们组合成一个转换管道（transformation pipeline），以便对图像数据进行预处理和标准化：
- torchvision.transforms.ToTensor()：图像数据转换为PyTorch张量（tensor），同时将像素值缩放到 [0, 1] 的范围内
- torchvision.transforms.Normalize((0.1307,), (0.3081,))：对图像数据进行标准化，即将每个通道的像素值减去均值（0.1307）并除以标准差（0.3081），以使得图像数据的分布接近标准正态分布
shuffle：为True表示打乱数据

观察测试数据

examples = enumerate(test_loader)
batch_idx, (example_data, example_targets) = next(examples)
print(example_targets)
print(example_data.shape)

// 图片实际对应的数字标签
tensor([3, 9, 4, 9, 9, 0, 8, 3, 1, 2, 3, 9, 1, 3, 6, 6, 4, 4, 9, 7, 3, 7, 6, 3,
         ......
        5, 7, 2, 0, 0, 2, 3, 1, 1, 5, 8, 5, 3, 9, 7, 6])
// 一批测试数据是一个形状张量，是1000个例子的28x28像素的灰度
torch.Size([1000, 1, 28, 28])

构建网络

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
        self.conv2_drop = nn.Dropout2d()
        self.fc1 = nn.Linear(320, 50)
        self.fc2 = nn.Linear(50, 10)

    def forward(self, x):
        x = F.relu(F.max_pool2d(self.conv1(x), 2))
        x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
        x = x.view(-1, 320)
        x = F.relu(self.fc1(x))
        x = F.dropout(x, training=self.training)
        x = self.fc2(x)
        return F.log_softmax(x, dim=1)

self.conv1 = nn.Conv2d(1, 10, kernel_size=5)表示第一个卷积层，输入通道为1（灰度图像），输出通道为10，卷积核大小为5x5
self.conv2_drop = nn.Dropout2d()表示二维的dropout层，用于在训练过程中随机地将输入张量的部分元素设置为0，以减少过拟合
self.fc1 = nn.Linear(320, 50)：全连接层1，输入大小为320，输出大小为50
forward(self, x)：神经网络的前向传播函数，用于定义输入数据在网络中的流动和计算过程
- F.relu(F.max_pool2d(self.conv1(x), 2))：将输入 x 传入第一个卷积层 self.conv1 中进行卷积操作，然后应用 ReLU 激活函数，并通过最大池化操作缩小特征图的尺寸
- x = x.view(-1, 320): 将特征图展平为一维向量，以便输入到全连接层 self.fc1，-1 表示将剩余维度自动调整为使得展平后的大小为320
- x = F.relu(self.fc1(x))：将展平后的特征向量x传入全连接层self.fc1中，并应用ReLU激活函数，将卷积层提取的特征映射到一个较低维度的空间
- x = F.dropout(x, training=self.training)应用 dropout 操作，随机地将部分神经元的输出设置为0，以减少过拟合。training=self.training参数表示只在训练模式下应用 dropout，而在测试模式下不应用
- x = self.fc2(x)将经过 dropout 操作的特征向量 x 传入全连接层 self.fc2 中，得到最终的分类结果
- return F.log_softmax(x, dim=1)对全连接层 self.fc2 的输出进行 log_softmax 操作，以得到预测的类别概率分布

# 初始化网络和优化器
network = Net()
optimizer = optim.SGD(network.parameters(), lr=learning_rate, momentum=momentum)

模型训练

train_losses = []
train_counter = []
test_losses = []
test_counter = [i * len(train_loader.dataset) for i in range(n_epochs + 1)]

train_losses：记录训练过程中的损失值
train_counter：用于记录训练过程中的批次数
test_losses：用于记录测试过程中的损失值
test_counter：在训练了 0、1、2、…、n_epochs 个 epoch 后进行测试的样本数

def train(epoch):
    network.train()
    for batch_idx, (data, target) in enumerate(train_loader):
        optimizer.zero_grad()
        output = network(data)
        loss = F.nll_loss(output, target)
        loss.backward()
        optimizer.step()
        if batch_idx % log_interval == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'
                  .format(epoch, batch_idx * len(data),len(train_loader.dataset), 
                          100. * batch_idx / len(train_loader),loss.item()))
            train_losses.append(loss.item())
            train_counter.append((batch_idx * 64) + ((epoch - 1) * len(train_loader.dataset)))
            torch.save(network.state_dict(), './model.pth')
            torch.save(optimizer.state_dict(), './optimizer.pth')

network.train(): 将神经网络模型设置为训练模式
optimizer.zero_grad(): 清零优化器的梯度缓存。每次迭代中，梯度都会累积，所以在每个批次开始时需要将梯度清零
loss = F.nll_loss(output, target)：计算模型预测结果 output 与真实标签 target 之间的损失。在这里，采用的损失函数是负对数似然损失(Negative Log Likelihood，NLL)。这个损失函数通常用于多类别分类任务，并且在模型最后一层没有应用 softmax 激活函数的情况下使用
loss.backward()：反向传播损失，计算参数的梯度。这一步将计算出损失函数对网络中所有参数的梯度
optimizer.step()：根据计算出的梯度更新模型的参数。这一步是优化器的核心步骤，它会根据梯度更新模型参数，使得损失函数尽可能减小
train_losses.append(loss.item())：将当前批次的损失值记录到 train_losses 列表中
(batch_idx * 64) + ((epoch - 1) * len(train_loader.dataset))记录当前批次的索引，这个索引表示当前已经处理的样本数

def test():
    network.eval()
    test_loss = 0
    correct = 0
    with torch.no_grad():
        for data, target in test_loader:
            output = network(data)
            test_loss += F.nll_loss(output, target, reduction='sum').item()
            pred = output.data.max(1, keepdim=True)[1]
            correct += pred.eq(target.data.view_as(pred)).sum()
    test_loss /= len(test_loader.dataset)
    test_losses.append(test_loss)
    print('\nTest set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

network.eval()：将神经网络模型设置为评估模式，这一步是为了确保在测试过程中不会应用训练过程中的一些特定于训练的操作，例如 dropout 和批量归一化。在评估模式下，模型的行为会略有不同，以便更准确地评估模型在测试数据上的性能
with torch.no_grad()表示在该代码块中计算的梯度不会被保存，从而节省内存并加快计算速度
test_loss += F.nll_loss(output, target, reduction='sum').item()：计算模型对当前批次测试数据的损失，并累积到 test_loss 中，这里采用的损失函数是负对数似然损失（Negative Log Likelihood，NLL）
pred = output.data.max(1, keepdim=True)[1]：从模型的输出中获取预测类别
correct += pred.eq(target.data.view_as(pred)).sum()：统计模型在当前批次上预测正确的样本数量
test_loss /= len(test_loader.dataset)：计算平均测试损失

训练结果如图

检查点的持续训练

# 初始化一组新的网络和优化器
continued_network = Net()
continued_optimizer = optim.SGD(network.parameters(), lr=learning_rate, momentum=momentum)
# 加载网络的内部状态，并在最后一次保存它们时优化它们
network_state_dict = torch.load('model.pth')
continued_network.load_state_dict(network_state_dict)
optimizer_state_dict = torch.load('optimizer.pth')
continued_optimizer.load_state_dict(optimizer_state_dict)

for i in range(4, 9):
    test_counter.append(i * len(train_loader.dataset))
    train(i)
    dtest()

新增几轮训练之后的测试结果：

术语概念解释

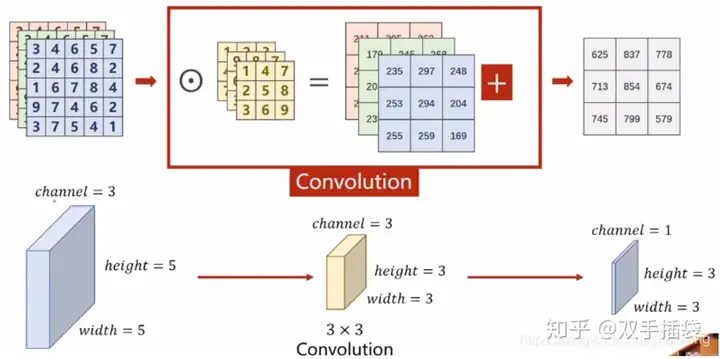
卷积（Convolution)：

从一个小小的权重矩阵，也就是卷积核（kernel）开始，让它逐步（从左至右，从上至下）在二维输入数据上“扫描”。卷积核“滑动”的同时，计算权重矩阵和扫描所得的数据矩阵的乘积（注意这里是两个矩阵对应数据相乘再把所有结果相加，不是矩阵乘法！！！），然后把结果汇总成一个输出像素。

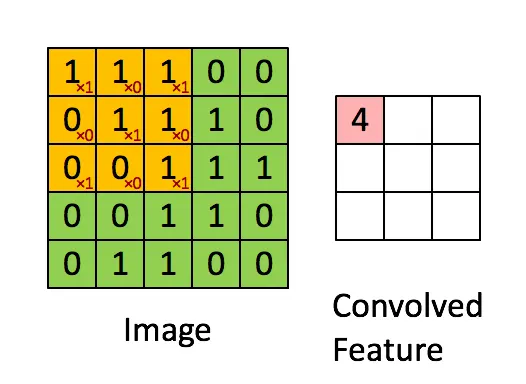
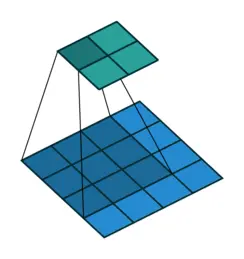
填充（Padding）：

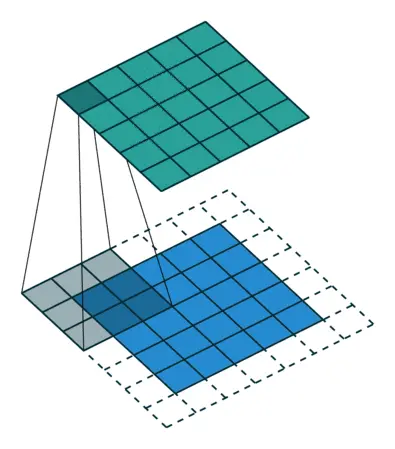
前面可以发现，输入图像与卷积核进行卷积后的结果中损失了部分值，输入图像的边缘被“修剪”掉了（边缘处只检测了部分像素点，丢失了图片边界处的众多信息）。这是因为边缘上的像素永远不会位于卷积核中心，而卷积核也没法扩展到边缘区域以外。

为解决这个问题，可以在进行卷积操作前，对原矩阵进行边界填充（Padding），也就是在矩阵的边界上填充一些值，以增加矩阵的大小，通常都用“0”来进行填充的（如图中矩形外围的虚线框）。

常用的两种padding：

（1）valid padding：不进行任何处理，只使用原始图像，不允许卷积核超出原始图像边界

（2）same padding：进行填充，允许卷积核超出原始图像边界，并使得卷积后结果的大小与原来的一致

步长(Stride)：

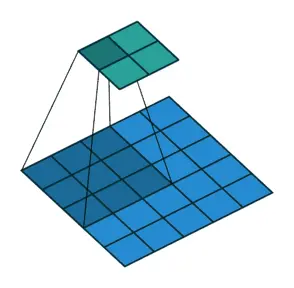
滑动卷积核时，我们会先从输入的左上角开始，每次往左滑动一列或者往下滑动一行逐一计算输出，我们将每次滑动的行数和列数称为Stride，在之前的图片中，Stride=1；在下图中，Stride=2。

步长Stride的作用：成倍缩小尺寸，而这个参数的值就是缩小的具体倍数，比如步幅为2，输出就是输入的1/2；步幅为3，输出就是输入的1/3。

TIPS

卷积核的大小一般为奇数*奇数 1*1，3*3，5*5，7*7都是最常见的。这是为什么呢？为什么没有偶数*偶数？

（1）更容易padding

在卷积时，我们有时候需要卷积前后的尺寸不变。这时候我们就需要用到padding。假设图像的大小，也就是被卷积对象的大小为n*n，卷积核大小为k*k，padding的幅度设为时，卷积后的输出就为，即卷积输出为n*n，保证了卷积前后尺寸不变。但是如果k是偶数的话，(k-1)/2就不是整数了。

（2）更容易找到卷积锚点

在CNN（卷积神经网络）中，进行卷积操作时一般会以卷积核模块的一个位置为基准进行滑动，这个基准通常就是卷积核模块的中心。若卷积核为奇数，卷积锚点自然就是卷积核模块中心，但如果卷积核是偶数，这时候就没有办法确定了。

IMPORTANT

卷积的计算公式

输入图片的尺寸：一般用 n×n 表示输入的image大小。

卷积核的大小：一般用 f×f 表示卷积核的大小。

填充（Padding）：一般用 p 来表示填充大小。

步长(Stride)：一般用 s 来表示步长大小。

输出图片的尺寸：一般用 o 来表示。

如果已知 n 、f 、p、s 可以求得 o ，计算公式如下：

其中”⌊ ⌋”是向下取整符号，用于结果不是整数时进行向下取整。

多通道卷积

上述例子均为单通道图像。实际上，大多数输入图像都有 RGB 3个通道。

这里就要涉及到“卷积核”和“filter”这两个术语的区别。在单通道的情况下，“卷积核”就相当于“filter”，这两个概念是可以互换的。但在一般情况下，它们是两个完全不同的概念。每个“filter”实际上恰好是“卷积核”的一个集合，在当前层，每个通道都对应一个卷积核，且这个卷积核是独一无二的。

最大池化是一种常用的池化操作，用于在卷积神经网络中对特征图进行下采样。它的作用是通过保留特征图中每个区域的最大值来减小特征图的空间大小，从而减少计算量并提取最显著的特征。

池化层每次在一个池化窗口上计算输出，然后根据步幅移动池化窗口。下图是目前最常用的池化层，步幅为2，池化窗口为2×2的二维最大池化层。每隔2个元素从图像划分出2×2的区块，然后对每个区块中的4个数取最大值。这将会减少75%的数据量。

Quick facts of PyTorch

torch.nn.Linear

torch.nn.Linear 是PyTorch中的一个模块，用于实现全连接层（也称为线性层）。它接受一个输入向量并将其映射到输出向量，通过学习权重矩阵和可选的偏置向量来完成这一过程。

torch.nn.Linear(in_features, out_features, bias=True, device=None, dtype=None)

in_features: 输入向量的特征数量。
out_features: 输出向量的特征数量。
bias: 如果设置为 True，则添加一个偏置项（默认为 True）。
device: 指定权重和偏置所在的设备（例如 ‘cpu’ 或 ‘cuda’），如果未指定，则使用默认的设备。
dtype: 指定权重和偏置的数据类型，如果未指定，则使用默认的数据类型。

torch.nn.Softmax

torch.nn.Softmax(dim=None)

将一组值转换成概率分布，其中每个值代表各个类别的概率。Softmax 函数的输出是一个概率向量，所有元素之和为 1。维度参数 dim，该参数指定应用 Softmax 函数的维度

torch.nn.AdaptiveAvgPool1d

对输入张量应用一个1维适应平均池化层

torch.nn.AdaptiveAvgPool1d(output_size)

Input: or .
Output: or , where $Extra close brace or missing open braceL_{out}=output{_}size$ .

torch.nn.AdaptiveAvgPool2d

对输入张量应用一个2维适应平均池化层

torch.nn.AdaptiveAvgPool2d(output_size)

Input: or .
Output: or , where $Extra close brace or missing open braceS=output{_}size$ .

torch.nn.functional.dropout

torch.nn.functional.dropout(input, p=0.5, training=True, inplace=False)

以 p 的概率随机将输入中的一些元素清零，这是一种正则化技术，有助于防止过拟合

torch.nn.Conv2d

torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)

二维卷积层
Input: or
Output: or , where

,

torch.nn.BatchNorm2d

torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True, device=None, dtype=None)

用于对二维卷积网络中的特征图进行批量归一化(batch normalization)。批量归一化是一种加速训练过程并提高模型泛化能力的技术。

Input: (N,C,H,W)
Output: (N,C,H,W) (same shape as input)

torch.nn.LeakyReLU

torch.nn.LeakyReLU(negative_slope=0.01, inplace=False)

Leaky ReLU 是 ReLU 的一种变体，旨在解决 ReLU 函数在输入为负数时梯度消失的问题。Leaky ReLU 允许负数输入以较小的斜率通过，而不是完全阻止它们。

torch.bmm

用于执行批量矩阵乘法

torch.bmm(input, mat2, *, out=None)

input: 第一个三维张量，形状为 (batch_size, m, k)。
mat2: 第二个三维张量，形状为 (batch_size, k, n)。
out: 可选参数，用于存储结果的输出张量。

返回一个三维张量，形状为 (batch_size, m, n)，其中每个 (m, n) 矩阵是对应批次中的两个输入矩阵的乘积

torch.Tensor.view

返回与原张量具有相同数据但形状不同的新张量

>>> x = torch.randn(4, 4)
>>> x.size()
torch.Size([4, 4])
>>> y = x.view(16)
>>> y.size()
torch.Size([16])
>>> z = x.view(-1, 8)  # the size -1 is inferred from other dimensions
>>> z.size()
torch.Size([2, 8])

如果某一输入为 -1 ，则表示当前值根据其他维度的值计算，例如上面代码中的z = x.view(-1, 8)

torch.unsqueeze

torch.unsqueeze(input, dim)

>>> x = torch.tensor([1, 2, 3, 4])
>>> torch.unsqueeze(x, 0)
tensor([[ 1,  2,  3,  4]])

返回一个在指定位置插入一个维度的新张量

torch.squeeze

在指定维度上降维，若不指定具体位置，怎将当前所有维度为1的维度删除。若给定位置上维度不为1，则操作无效

forward

forward函数是定义神经网络模型的核心部分。它是torch.nn.Module子类中的一个方法，用于定义数据通过模型的前向传播过程。当您创建一个自定义的神经网络模型时，通常需要继承torch.nn.Module类，并实现forward方法。

forward函数的作用

定义前向传播逻辑：
- forward函数定义了输入数据如何流经网络中的各个层，包括线性变换、卷积、激活函数等。
- 这个函数决定了模型架构。
自动计算梯度：
- PyTorch通过跟踪forward函数中的操作来构建计算图，从而能够自动计算梯度。
- 当调用backward方法时，计算图会被用来反向传播误差，并更新权重。

Leostar's Blog